Fred Jonasson administra la granja de su familia. Para complementar varios alimentos que se cultivan en la granja, Fred también cría cerdos para venta y desea determinar las cantidades de los distintos tipos de alimento disponibles (maíz, grasas y alfalfa) que debe dar a cada cerdo.

Como éstos se comerían cualquier mezcla de estos tipos de alimento, el objetivo es determinar cuál de ellas cumple ciertos requisitos a un costo mínimo.

En la siguiente tabla se presentan las unidades de cada tipo de ingrediente nutritivo básico que contiene 1 kilogramo de cada tipo de alimento, junto con los requisitos de nutrición diarios y los costos de los alimentos:

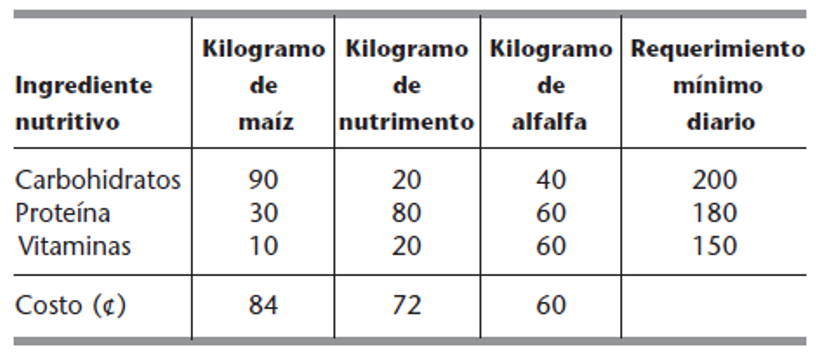
a) Formule el modelo de programación lineal para este problema.

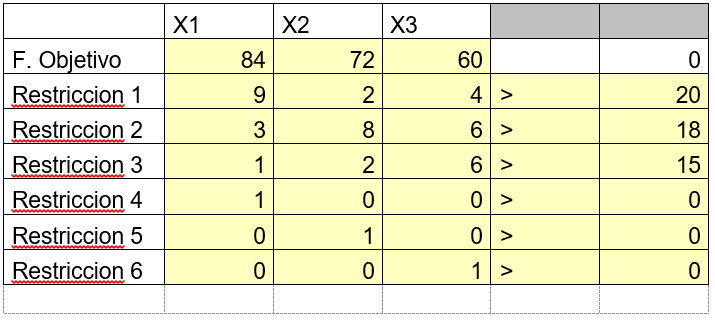
b) Despliegue el modelo en una hoja de Excel.

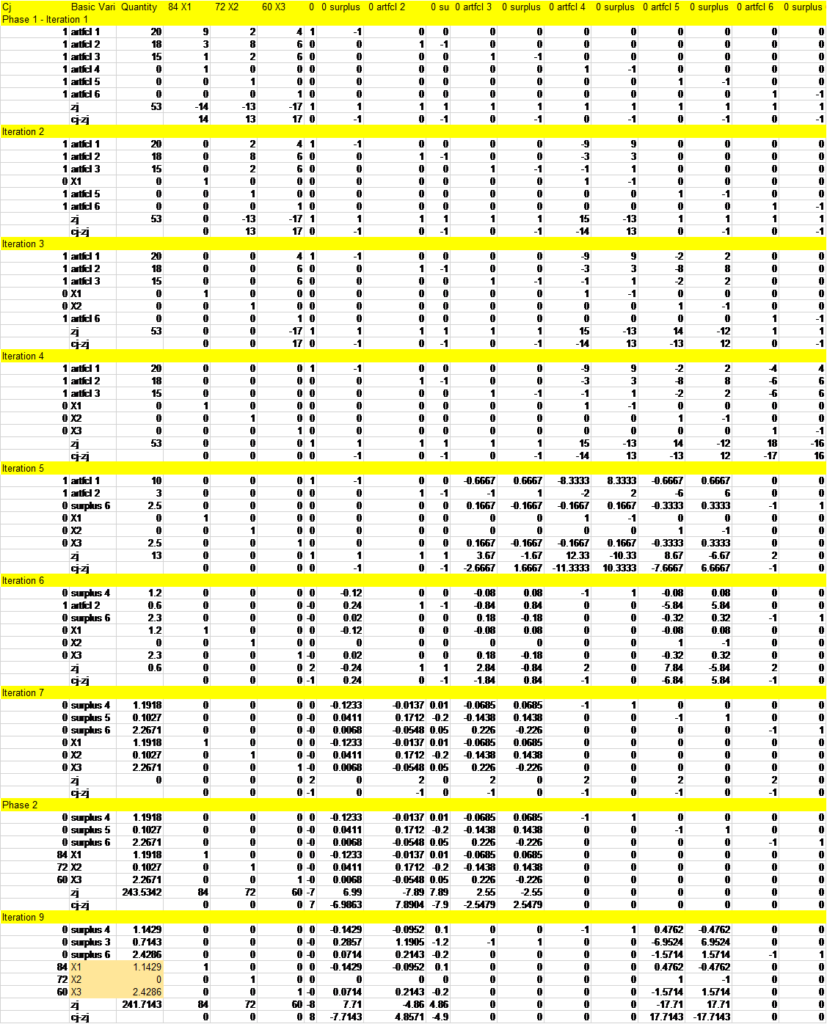
La solución optima es de x1= 1.1429,x2=0 y x3=2.42

c) Utilice la hoja de cálculo para verificar: si (x1,x2,x3)=(1,2,2) es factible y, si lo es, cuál sería el costo diario de esta dieta.

¿Cuántas unidades de cada ingrediente nutritivo proporciona al día esta dieta?

Cuando x1=1, x2=2 y x3=2

9(1) + 2(2)+ 4(2) >=20 Si

3(1) + 8(2) + 6(2) >=18 Si

1(1) + 2(2) + 6(2) >=15 Si

Con este modelo también se cumplen las restricciones y proporcionan de 21 de carbohidratos = 210

31 de proteínas =310

17 de vitaminas =170

Total de costo diario= 690

d) Tome unos minutos para usar un enfoque de prueba y error con la hoja de cálculo a fin de obtener la mejor estimación de la solución óptima. ¿Cuál es el costo diario de su solución?

La solución optima es de x1= 1.1429,x2=0 y x3=2.42

9(1.1429) + 2(0)+ 4(2.42) >=20 No

3(1.1429) + 8(0) + 6(2.42) >=18 No

1(1.1429) + 2(0) + 6(2.42) >=15 No

No se cumplen las restricciones y proporcionan de 19.96 de carbohidratos = 199.60

17.94 de proteínas = 179.40

14.52 de vitaminas = 145.20

Total de costo diario = 524.20

e) Use el Excel Solver para resolver el modelo por el método simplex.

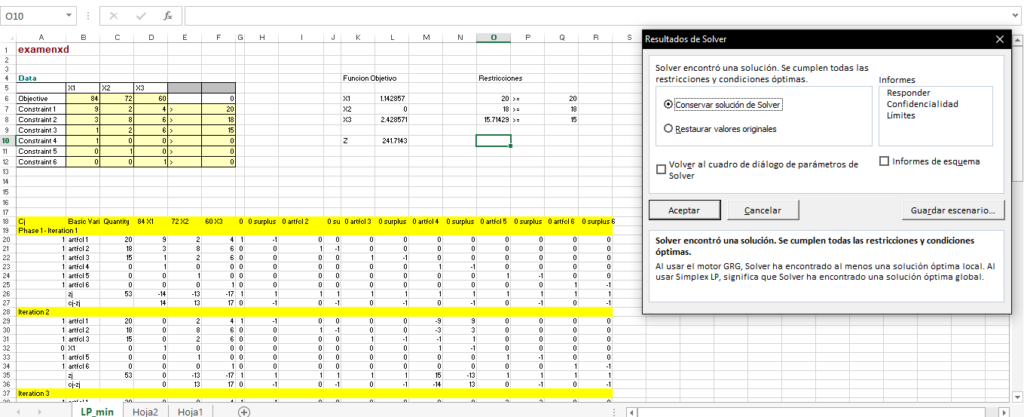
Los resultados fueron de x1=1.14,x2=0 y x3= 2.42